If you were to guess the missing part of the sentence — “My name John Doe” what would you guess? Most people would answer this with an “is.” (A few interesting breeds would go for a “was” as well) You essentially guess a word that has the highest probability of being there. Interestingly enough, machines also work the same way. However, they don’t understand these words in their textual form. These words need to be converted into numbers for a machine to understand. How do we do it? The answer is Word embeddings.

Consider the below sentences -

Hi, how are you? Hello, how is it going? In this context, “Hi” and “Hello” carry the same meaning. If we were to organize words based on their semantic roles, “Hi” and “Hello” would naturally be grouped together.

This semantic similarity can be represented mathematically as well. If somehow plotted in an n-dimensional space, these words would be plotted closer to each other.

If n = 3, It would look something like this -

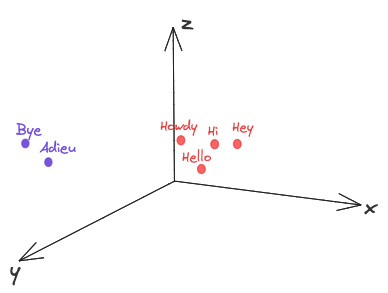
Each word here must have an (x,y,z) coordinate. These sets of coordinates are nothing but Word Embeddings. By a technique called Word2Vec, we can transform these words into corresponding embeddings, so that these can be fed to a Neural Network. We can apply the same logic to graphs as well, where the nodes that are in proximity would appear closer in the vector space.

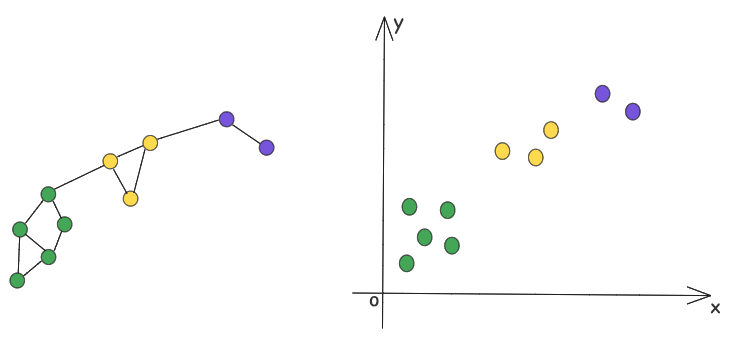
Word2Vec when applied on graphs, is called DeepWalk, developed by Bryan Perozzi, Rami Al-Rfou, and Steven Skiena. DeepWalk, like word2vec, is an unsupervised learning approach that captures the neighborhood similarity of nodes in a graph. Let's create a simple implementation of this technique in Clojure.

Graph representation

We will use a representation similar to an adjacency list.

(defn create-graph
  "Create a graph from a sequence of edges"
  [edges]
  (reduce (fn [graph [u v]]
            (-> graph
                (update u (fnil conj #{}) v)
                (update v (fnil conj #{}) u)))
          {}
          edges))
          
 => (create-graph [[:a :b] [:a :c] [:b :c] [:b :d]])
 => {:a #{:c :b}, :b #{:c :d :a}, :c #{:b :a}, :d #{:b}}

It is a map containing the nodes as keys and corresponding values being the set of connected nodes.

Initializing embeddings

We will initialize the embeddings with random values and by a stochastic, unsupervised process, we will gradually make our way towards more accurate values.

(defn init-embedding
  "Creates random embedding for size m x n where m = # of nodes, n =  vector-size"
  [vector-size vocab-size]
  (->> rand
       ((partial repeatedly vector-size))
       (partial vec)
       ((partial repeatedly vocab-size))
       vec))

Random walk

It's like taking a stroll through the city, where buildings represent the nodes and edges represent the roads. We decide how many buildings we want in the walk and start walking from a fixed building. At the end of each walk, we attempt to make sense of which buildings were close to each other.

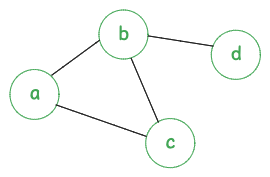
For the undirected graph above, let's say the starting node is "a" and the walk length is 3. The random walks will be -

1. a → b → c
2. a → c → b
3. a → b → d

(defn get-neighbors
  "Get neighbors of a node in the graph"
  [graph node]
  (get graph node))


(defn random-walk
  "Generate a random walk of length 'walk-length' starting from 'start-node'"
  [graph start-node walk-length]
  (loop [walk [start-node]
         current-node start-node
         steps-left (dec walk-length)]
    (if (zero? steps-left)
      walk
      (let [neighbors (get-neighbors graph current-node)
            next-node (rand-nth (seq neighbors))]
        (recur (conj walk next-node)
               next-node
               (dec steps-left))))))

For each walk, we will train the model on the words appearing in the random walk. The objective is to maximize the dot product between the vector representations of nodes that appear nearby within these walks. This approach leverages the fact that the dot product is proportional to the cosine similarity between vectors. By increasing the dot product of vectors representing nearby nodes, we encode the graph's local structure into the embedding space. Nodes that frequently co-occur in random walks will develop similar vector representations, effectively capturing the graph's topology in a continuous vector space.

Training process

For this example, we are considering only positive samples, hence the error is calculated as - (- 1 (sigmoid dot_product)) The gradients are calculated using this error and the current vectors. Both the word vector and the context vector are updated in the direction that reduces the error.

(defn train-pair
  "Train on a single word pair"
  [word context learning-rate vocab vectors]
  (let [word-idx (get vocab word)
        context-idx (get vocab context)
        word-vec (get vectors word-idx)
        context-vec (get vectors context-idx)
        dot-product (reduce + (map * word-vec context-vec))
        error (- 1 (sigmoid dot-product))
        word-delta (mapv #(* learning-rate error %) context-vec)
        context-delta (mapv #(* learning-rate error %) word-vec)]
    (-> vectors
        (update word-idx #(mapv + % word-delta))
        (update context-idx #(mapv + % context-delta)))))
        
        
(defn process-walk
  "trains the skip gram model for one random walk"
  [{:keys [walk embedding vocab window-size learning-rate]}]
  (reduce
   (fn [embedding [idx word]]
     (let [context-words (get-context-words idx walk window-size)]
       (reduce
        #(train-pair word %2 learning-rate vocab %1)
        embedding
        context-words)))
   embedding
   (map-indexed vector walk)))

This function is typically called many times during training, gradually refining the word vectors to capture semantic relationships between words based on their co-occurrence patterns in the text.

Results

(defn deepwalk
  "Run DeepWalk algorithm on the given graph"
  {:opts [:vector-size
          :walk-length
          :num-walks
          :window-size
          :learning-rate]}
  [edges & opts]
  (let [graph (gc/create-graph edges)
        trained-vectors (mc/train-deepwalk graph (apply hash-map opts))]
    {:graph graph
     :vectors trained-vectors}))

=> (deepwalk [[:a :b] [:a :c] [:b :c] [:b :d]]
             :vector-size 3
             :learning-rate 0.025)

=> {:graph {:a #{:c :b}, :b #{:c :d :a}, :c #{:b :a}, :d #{:b}},
     :vectors
     [[1.9573999686062304 0.5519261864300776 1.2504320597448482]
      [2.2479788168874233 0.6338604247877525 1.4360605023739048]
      [2.0522495736710527 0.5786708383394699 1.311024166074367]
      [1.8370678722080205 0.5179962609496533 1.1735611526405794]]}

This is a basic idea of implementing DeepWalk. A thing to note is that this implementation is a simplified version of Word2Vec. These results won't be the most accurate ones. A full implementation would include negative sampling (training for nodes that are farther away from each other), and subsampling of frequent words, and would be optimized for efficiency. Please find the full source code here - https://github.com/mihirrd/clj-deepwalk